Question Set 1 – Solve problems involving 1D motion
Questions :
(a) What is the magnitude of the average acceleration of a skier who, starting from rest, reaches a speed of 8.0 m/s when going down a slope for 5.0 s? (b) How far does the skier travel in this time?
A jogger accelerates from rest to 3.0 m/s in 2.0 s. A car accelerates from 38.0 to 41.0 m/s also in 2.0 s. (a) Find the acceleration (magnitude only) of the jogger. (b) Determine the acceleration (magnitude only) of the car. (c) Does the car travel farther than the jogger during the 2.0 s? If so, how much farther?
A jetliner, traveling northward, is landing with a speed of 69 m/s. Once the jet touches down, it has 750 m of the runway in which to reduce its speed to 6.1 m/s. Compute the average acceleration (magnitude and direction) of the plane during landing.
An athlete takes 20 s to reach his maximum speed of 180 km/h. What is the magnitude of his average acceleration?
An object having a velocity 4.0 m/s is accelerated at the rate of 1.2 m/s2 for 5.0 s. Find the distance travelled during the period of acceleration.
A person traveling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s^22 to his scooter. How far will it travel before stopping?
A train starts from rest and moves with a constant acceleration of 2.0 m/s^22 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find (a) the total distance moved by the train, (b) the maximum speed attained by the train, and (c) the position of the train at half the maximum speed.
A bullet traveling with a velocity of 16 m/s penetrates a tree trunk and Comes to rest in 0.4 m. Find the time taken during the deceleration.
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed of 18.0 km/h find (a) the average velocity during this period, and (b) the distance traveled by the particle during this period.
Explanations :
(a) What is the magnitude of the average acceleration of a skier who, starting from rest, reaches a speed of 8.0 m/s when going down a slope for 5.0 s? (b) How far does the skier travel in this time?
a. From Equation (1), the definition of average acceleration, the magnitude of the average acceleration of the skier is
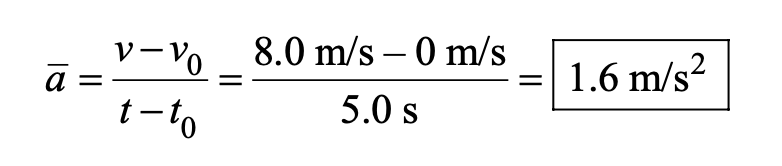
b. With x representing the displacement traveled along the slope, From equation (2)
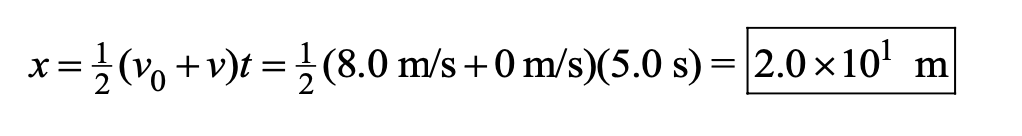
a. The magnitude of the acceleration can be found from Equation 1 (v = v0 + at) as
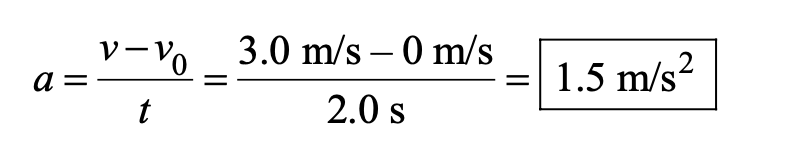
b. Similarly, the magnitude of the acceleration of the car is
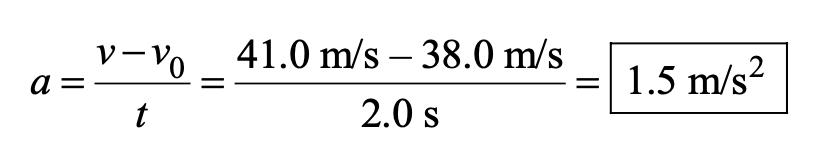
c. Assuming that the acceleration is constant, the displacement covered by the car can be found from Equation (v^2 = v0^2 + 2ax):
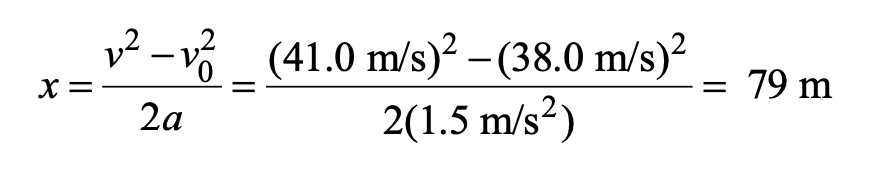
Similarly, the displacement traveled by the jogger is
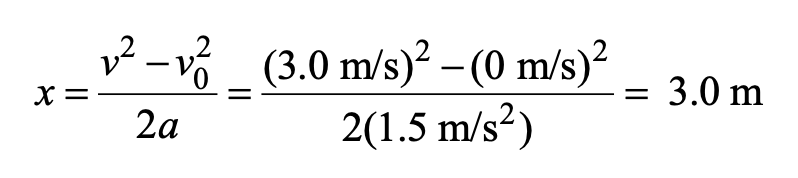
Therefore, the car travels 79 m – 3.0 m = 76 m further than the jogger.
The average acceleration of the plane can be found by solving Equation (v^2 = v0^22 + 2ax) for a. Taking the direction of motion as positive, we have
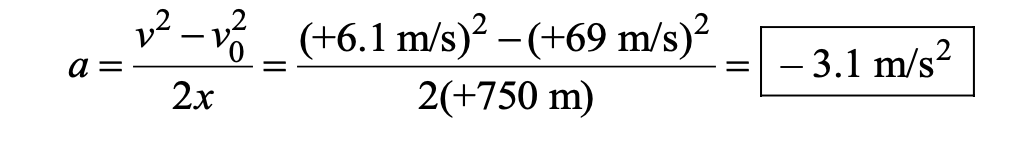
The minus sign indicates that the direction of the acceleration is opposite to the direction of motion, and the plane is slowing down.
Initial velocity, v0 = 0
Final velocity, v = 180 km/h = 50 m/s and Time, t = 20 s
We know, v = v0 + at
Where v = final velocity, v0 = initial velocity, a = acceleration and t= time
or a = (v-v0)/t = 50/20 = 2.5 m/s^2
Initial velocity = v0 = 4.0 m/s
Time = t = 5.0 s
Acceleration = a = 1.2 m/s^2
The distance travelled,
x = v0t + 1/2 at^22
= 4x 5 + 1/2 x 1.2 x 5 x 5
= 35 m
Initial velocity = v0 = 43.2 km/h = 12 m/s
Final velocity = v = 0 km/h
Acceleration = a = -6.0 m/s^22
Using relation, v^2 = v0^22 + 2ax
v^2 – v0^2 = 2ax
-144= -12 x
or x = 12 m
Hence person will travel 12 m before stopping
For the first half minute :
Initial velocity = v0 = 0
Acceleration = a = 2 m/s^22
v = Final velocity before apply breaks and time, t= 30 sec
v = v0 + at = 0 + 60 = 60 m/s
(a)
Distance covered before applying the brake
x1 = v0t + 1/2 at^2 = 900 m
When the brake is applied, the final velocity before braking becomes the initial velocity for after braking.
After braking,
Initial velocity, v01 = 60 m/s (when break applied)
Final velocity v1 = 0
and at t = 60 sec
Distance travelled, x2 =v0t+1/2at^2
a1 = (1-v01)/t = -1 m/s^2
and x2 = 1800 m
Therefore, total distance travelled by train = x1+x2 = 2700 m or 2.7 km
Initial velocity= v0 = 16 m/s
Distance covered = x = 0.4 m
Time, t=?
We know acceleration,
a = (v^2-v0^2)/2x = (0-162)/(2×0.4)
= -320 m/s^2
Also, t = (v-v0)/a
= (0-16)/-320 = 0.05 sec
Initial velocity = v0 = 0 m/s
Final velocity = v = 18 km/h = 5 m/s and
Time = t = 5 sec
Now,
a = (v-v0)/t = 5/5 = 1 m/s2
Consider, x be the travelled distance, so x = v0t + 1/2 at^2 = 12.5 m
(a) Average velocity = (12.5)/5 = 2.5 m/s
(b) Distance travelled = 12.5 m
